- théorème
-
théorème [ teɔrɛm ] n. m.• 1539; lat. theorema, mot gr. « objet d'étude, principe », de theôrein→ théorie♦ Proposition démontrable qui résulte d'autres propositions déjà posées (opposé à définition, axiome, postulat, principe). Démontrer un théorème. ⇒ démonstration. Théorème de géométrie, de mathématique. Le théorème de Pythagore. — « Tout ce qui précédait n'avait été dit que pour en venir là; c'était comme une espèce de théorème : C. Q. F. D. » (Larbaud).
● théorème nom masculin (bas latin theorema, du grec theôrêma, de theôreîn, examiner) Proposition scientifique qui peut être démontrée. Expression d'un système formel démontrable à l'intérieur de ce système.théorème⇒THÉORÈME, subst. masc.A. — LOG., MATH. [P. oppos. à axiome, postulat] Proposition qui peut être démontrée par un raisonnement logique à partir de faits donnés ou d'hypothèses justifiables. Théorème réciproque; théorème d'arithmétique, de géométrie, de mécanique; théorème de Thalès; démontrer un théorème. Il serait fort extraordinaire, et par cela seul improbable, que tant de géomètres, depuis plus de vingt siècles, se fussent trompés en trouvant irréprochable la démonstration du théorème de Pythagore, telle qu'on la lit dans Euclide (COURNOT, Fond. connaiss., 1851, p. 113). C'est dans une note de 1921, qu'E. Borel a jeté les premières bases de la théorie des jeux stratégiques. Il y présentait un cas particulier de ce que l'on appelle le théorème fondamental (en vertu duquel un maximum se trouve égaler un minimum) dont la démonstration fut donnée en 1928 par J. Von Neumann (Hist. gén. sc., t. 3, vol. 2, 1964, p 117).B. — P. ext. Énoncé reposant sur une démonstration rigoureuse. À la dernière dominicale, il soutenait que tout désir a droit à sa satisfaction; tous de trouver les corollaires du théorème, et le plafond n'a pas croulé! (PÉLADAN, Vice supr., 1884, p. 166). L'opuscule de la crise de l'esprit, sans doute le seul théorème intellectuel issu de la guerre qui tient compte de toutes les phases de l'événement (DU BOS, Journal, 1922, p. 139).REM. Théorématique, adj., épistémol. Qui a le caractère d'un théorème. Sciences théorématiques. Sciences énonçant des rapports hypothétiques, des lois. Les sciences théorématiques s'opposent aux sciences historiques, qui ont pour objet les faits; et aux sciences « économiques », c'est-à-dire aux sciences normatives (LAL. 1968).Prononc. et Orth.: [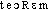
]. Voy. longue dans syll. finale ds PASSY 1914, BARBEAU-RODHE 1930, MARTINET-WALTER 1973 (4/17). MARTINET-WALTER [teo-] (4/17). Ac. 1694, 1718: theoreme, dep. 1740: théorème. Étymol. et Hist. 1. 1539 « proposition scientifique qu'une démonstration rend évidente » (J. CANAPPE, Le Troisième livre de la méthode thérapeutique, 19 ds Fr. mod. t. 19, p. 200); 2. 1930 « énoncé d'une proposition déduite logiquement à partir de faits explicites ou d'hypothèses justifiables » la découverte d'un théorème nouveau (RUYER, Esq. philos. struct., p. 254). Empr. au lat. d'époque impériale theorema « proposition », gr. 
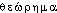« ce qu'on peut contempler; objet d'étude et de méditation », dér. de 
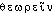« observer, contempler ». Fréq. abs. littér.:171. Bbg. BALDINGER (K.). Zum Übergang von der lat. zur frz. Fachterminologie im 14. Jahrht. Z. rom. Philol. 1975, t. 91, p. 486. — GOHIN 1903, p. 353.théorème [teɔʀɛm] n. m.ÉTYM. 1538; lat. theorema, grec theorema « objet d'étude, principe », de theôrein. → Théorie.❖1 Log., math. Proposition démontrable qui résulte d'autres propositions déjà posées (par oppos. à définition, axiome, postulat, principe). || Théorème réciproque. || Démontrer un théorème. ⇒ Démonstration. || Théorème de géométrie (→ Figure, cit. 5), de mécanique (→ Parallélogramme, cit.; résultante, cit. 1).2 Cour. (incorrect scientifiquement). Démonstration rigoureuse.0 Et, au bout de chaque fable, il y avait une morale, quelque réflexion bien plate et bien prosaïque qui nous donnait l'impression que tout ce qui précédait n'avait été dit que pour en venir là; c'était comme une espèce de théorème : C. Q. F. D.Valery Larbaud, Enfantines, « Devoirs de vacances », p. 205.❖DÉR. V. Théorématique.
Encyclopédie Universelle. 2012.
